Introduction：Particle size measurement of fine particles

Fine particles dispersed in a suspension or a solution usually have Brownian motion, which is slower for larger particles and faster for smaller particles. At this time, when the particles that are in Brownian motion are irradiated with laser light, the fluctuation of the scattered light according to the speed of each Brownian motion is observed.

In the dynamic light scattering method, as shown in Fig. 5, the particles dispersed in a solution are irradiated with laser light, and the scattered light is observed by the photon detector. At this time, the scattered light from the particles interferes with each other as shown in Young's optical interference experimental model (Fig. 6). Furthermore, since the particles are constantly moving in position due to Brownian motion, the intensity distribution due to the interference of scattered light is also constantly fluctuating. Therefore, if a pinhole or optical fiber optical system is used, this Brownian motion can be observed as fluctuations in scattered light intensity.

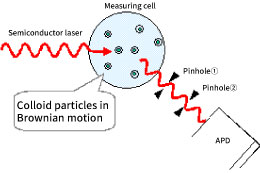
Figure 5. Schematic diagram of dynamic light scattering method

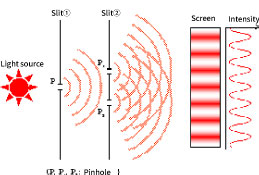
Figure 6. Young's optical interference experimental model

The observed chronological fluctuations of scattered light differ depending on the particle size, as shown in Fig. 7 and 8.

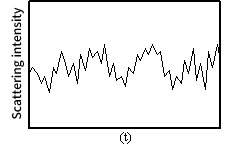
Figure 7. Fluctuation of scattered light of small particles

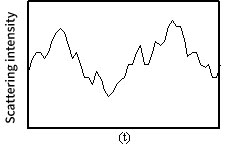
By observing this fluctuation, the autocorrelation function is obtained by the photon correlation method, and the cumulant method and the histogram method analysis are used to obtain diffusion coefficient indicating the Brownian motion velocity, and the particle size and particle size distribution.

The autocorrelation function is based on the scattering intensity I (t) at an arbitrary time (t), and the correlation for the scattering intensity I (t + τ) after (τ) time is expressed by the following equation.

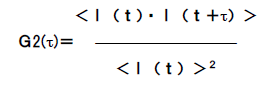
Here, <> represents the average. This autocorrelation function depends only on time (τ) and does not depend on measurement start time (t). In the autocorrelation function, when τ is small, the particles do not move much, so the change in the amount of scattered light is small and shows a high correlation, but when τ is large, the position of the particles becomes uncertain, so the amount of scattered light also changes randomly. The correlation is almost non-existent. Therefore, the resulting autocorrelation function is an exponential decay curve.

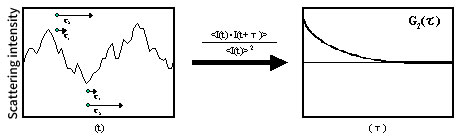
Figure 9. Scattered light intensity and autocorrelation function

The particles change their position by Brownian motion as shown in Fig.10. The autocorrelation function expresses the degree of particle overlap between τ1, τ2, τ3 ... from the position of particles at a certain reference time as a function of time. As a result, as shown in Fig. 11, the degree of overlap decreases with time, so the autocorrelation function G2 (τ) expresses a function that decays with time.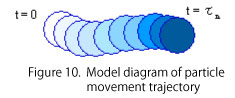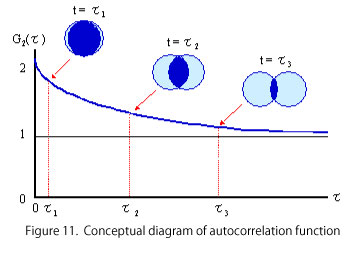

Refer to the materials of the 12th Scattering Study Group "Dynamic Light Scattering-Basic Seminar" by Professor Mitsuhiro Shibayama, Tokyo University

Analyzing the variation of scattering intensity using the photon correlation method yields a correlation function with a short correlation time for small particles and a long correlation function for large particles. The correlation function contains information about the translational Brownian motion of suspended particles, and the particle size and particle size distribution can be obtained by a calculation formula.

Figure 12. Fluctuations of scattered light from small particles and its autocorrelation function


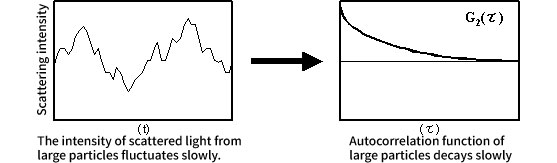
Figure 13. Fluctuations of scattered light from large particles and its autocorrelation function